| Brain Research Group >> Research >> Change-point analysis ... | << previous next >> |
When detection of the change-points in alpha band power was performed as in the previous subsection, more than one change-point per second was obtained in average. Such density of change-points may appear to be too high and it could be necessary to look for a way to reduce it---for example, if the segments between the change-points should be subjected to further analysis. The hypothesis of the hierarchy of EEG segmental descriptions (Kaplan 1998) (see subsection 7.3.2) is a theoretical reason for introducing the adjustment of the change-point detection probability. If the fine temporal structure of the EEG is studied, one may try to find as much change-points as possible, while taking into account constrains imposed by the properties of the analyzed EEG component (for example, in the case of a periodic process the temporal resolution may depend on its period). If the higher levels of the hierarchy of EEG segmental descriptions are studied, the most "powerful" change-points could be selected from a set of detected change-points corresponding to both more and less pronounced transformations of the signal, but it is more practical to adjust the detection procedure itself for the search of only most prominent changes.
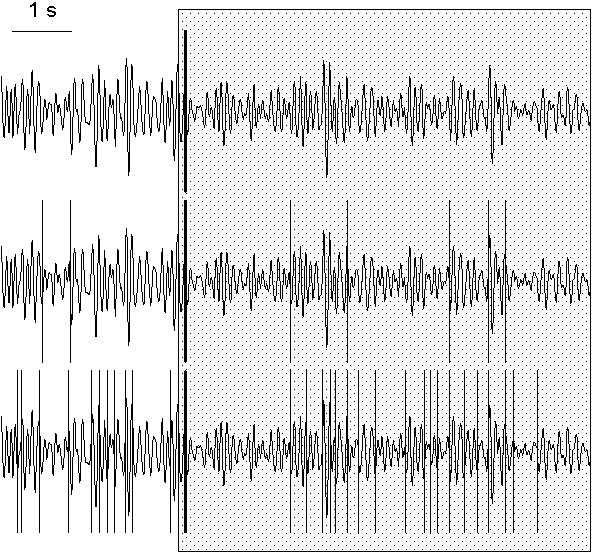
This problem can be solved in a number of ways. One of them is to operate by the "false alarm" probabilities, the method parameters which influence the probability of the decision about the presence of a change-point. An example is given in Fig. 7.5, where, in the same EEG interval, the number of change-points in alpha band power were found to be 1, 8 and 31 with three different sets of "false alarm" probabilities and with other method parameters unchanged.

Fig. 7.5. EEG filtered in alpha band (7.5--12.5 Hz) and change-points detected with different false alarm probability
The change-points (vertical lines) were detected in the basic diagnostic
sequence with the following "false alarm" probability sets: at the preliminary
estimation stage (0.2, 0.15, 0.1), (0.6, 0.5, 0.4), (0.8, 0.75, 0.7) for the
subintervals of
L ≥ 100, 50 ≤ L < 100 and 25 ≤ L < 50
correspondingly; at the rejection
stage (0.04, 0.02, 0.01), (0.4, 0.2, 0.1), (0.7, 0.6, 0.5) for the same
subinterval length ranges, correspondingly. For the convinience, the
change-points are shown against the same filtered EEG. Horizontal scale: 1 s.
The "strongest" change-point, which was found as the first one at the
preliminary estimation stage (solid vertical line), can be related to the
subject's reaction to the beginning of presentation of a highlighted image
(the period of presentation is shown by shaded area). The subject (tw09) was
asked to memorize the image.
To solve the problem is especially easy when only one, clearly most prominent change-point must be found in a given interval; this is the task solved in the above discussed work of Deistler et al. (1986) using parametric approach. With our procedure, it is sufficient to determine only the instant of the change-point which will be found the first on the stage of the preliminary estimation. The "false alarm" probability, as one may see from the algorithm, does not affect the order of detection of change-points at this stage. The only serious problem is that the most prominent change-point will be detected first only if it is located not at the periphery of the studied interval.
An example of the detection of single prominent change-point can be seen also in Fig. 7.5. In this figure, the change-point which was found first is shown as a thick line. This change-point corresponds to the beginning of the response of alpha rhythm to the presentation to a subject a luminous picture which he should memorize. The subject's alpha rhythm was slightly suppressed all the time when he saw the picture, nevertheless, it undergone considerable variations both before and during the presentation. The first change-point was found within approximately 150 ms after the beginning of the presentation and indicated the beginning of the period of suppressed alpha activity.
Another economical way of data processing, which leads to the reduction of the number of change-points and enables detection of only those which correspond to long-term transformations of the signal, is the compression (condensation) of the diagnostic sequence. Its simplest form is "thinning out" the data, i.e., the use, instead of a sequence x(t), a sequence x(kt), t=1,2, ... for some fixed k>1. To avoid the loss of information, averaging of data in successive windows can be used instead of "thinning out". The compression of the diagnostic sequence is especially effective in the analysis of the EEG recorded throughout night sleep. The EEG is an excellent indicator of sleep stages, because the electrical activity of the cortex strongly depends on them, but the analysis of sleep EEG is complicated by the huge amount of data to be processed (8 h of sleep means, if EEG is sampled with digitizing rate 100 Hz, 2,880,000 samples for each channel). The compression enables rapid detection of most prominent changes in such a recording (Fig. 7.6).
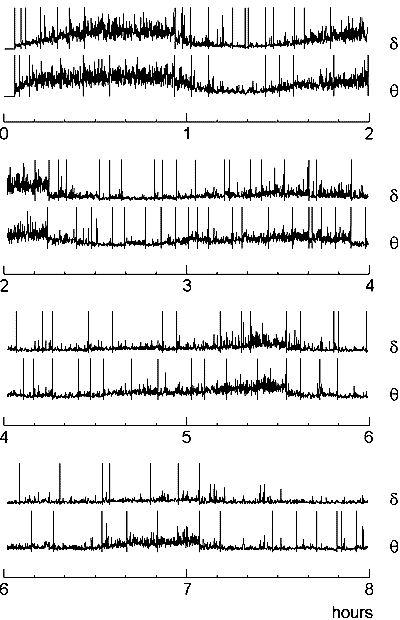
Fig. 7.6. Change-points in sleep EEG: an example of data compressing
EEG was recorded from right occipital electrode (O2) during 8 h of night sleep with sampling rate 400 Hz and downsampled to 20 Hz. After artefact edition the EEG was filtered in 1--4 Hz (delta) and 4--7 Hz (theta) frequency bands, the amplitude values were squared and then averaged in sequential non-overlaping windows (length 5 s, or 100 samples). The resulting sequences are shown (in each pair the upper curve is for theta band and the lower one is for delta) along with the change-points (vertical lines) detected in them.