| Brain Research Group >> Research >> Change-point analysis ... | << previous next >> |
In EEG signals registered simultaneously from different brain sites (see Fig. 7.7), change-points often appear close in time. A question arises of whether such near-coincidence of change-points could be used in estimating the synchrony of operating of different brain areas (Kaplan et al. 1995; Kaplan et al. 1997a; Kaplan et al. 1997c). This question, in its turn, brings up a number of new methodical issues, which will be discussed in this subsection. Below we will use the terms "coincidence" and "coinciding" instead of "near-coincidence" and "near-coinciding" for short.
For the detection of the change-points which will be used for the estimation of the synchrony, a higher "false alarm" probability can be used. It assures the lower probability of missing a change-point and, therefore, the higher number of change-points detected, making possible more accurate estimation of the level of change-point synchronization. The increase in the number of "false" change-points, in the present context, cannot strongly affect the results of the analysis. The "false" change-points contribute only to the fractions of non-coinciding and randomly coinciding change-points, but do not increase the number of systematically coinciding change-points. The number of randomly coinciding change-points (the noise level) can be easily estimated using the total numbers of change-points in each EEG channel, and thus the estimate of the number of systematically coinciding change-points can be cleared from the randomly coinciding change-points, both "true" and "false". One may see that the estimation of synchronization therefore includes a sort of additional validation of a change-point, which is taken into account only if "confirmed" by the presence of another change-point in a different EEG channel roughly simultaneously with the first one.
The estimation of change-point synchronization is essentially an analysis of synchronization of point processes. Such an analysis was well developed in neuroscience research, mainly in the investigations of impulse activity of single neurons (various methods are described in (Perkel et al. 1967; Gerstein et al. 1978; Gerstein et al. 1985; Palm et al. 1988; Aertsen et al. 1989; Gerstein et al. 1989; Frostig et al. 1990; Pinsky & Rinzel 1995). Surprisingly, this type of analysis has been completely ignored before in the EEG-based research (the only work we know is Guedes de Oliveira & Lopes da Silva 1980); this may be the result of lack of means for the extraction of such EEG "elements" which can be approximated by points.

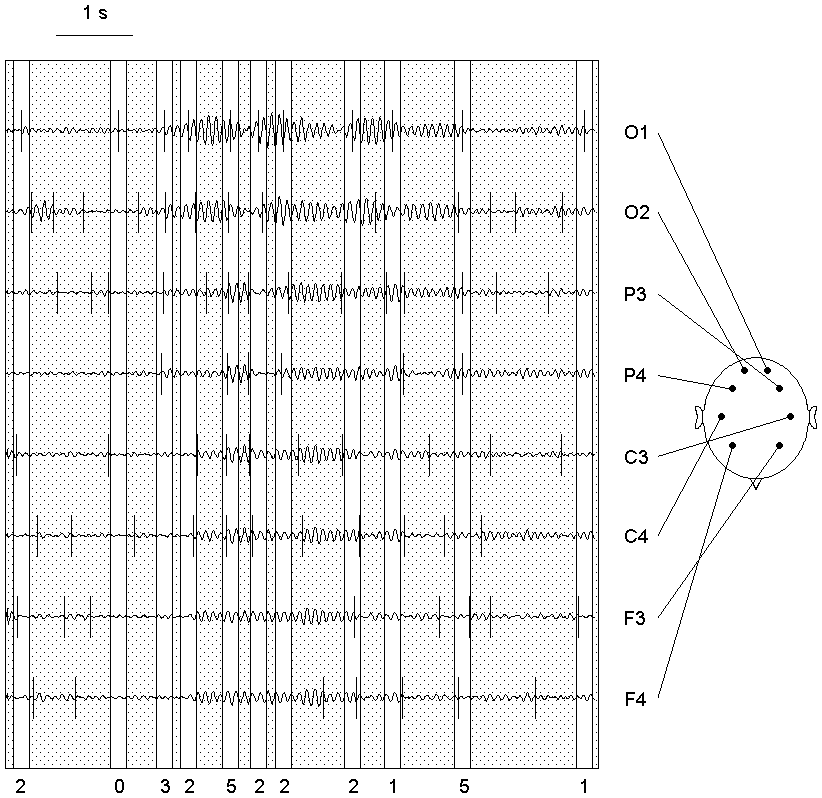
Fig. 7.9. Illustration for the analysis of change-point synchronization in multichannel EEG
Subject tw03, eyes closed. Each EEG channel was filtered with bandpass 7.5--12.5 Hz (alpha). The change-points were detected in the basic diagnostic sequence. For each change-point in channel O1 a time window (13 samples, or roughly 100 ms, from each side) is positioned. Below the chart the total number of change-points from other channels which fall into the window is shown. Such change-points are considered as coincided with the change-point in O1.
The most simple and, nevertheless, quite effective procedure is the use of some time threshold for the decision about the coincidence: change-points in different channels are considered as coinciding if the time distance between them does not exceed the time threshold. Fig. 7.9 illustrates this approach: each change-point in the first channel (left occipital electrode) is surrounded by a "window" (in this case, by 100 ms to each side from a change-point); all the change-points in other channels are thought to be coinciding if falling into this window. It turned out that these case are not rare, in spite of the fact that some of the change-points were detected in the intervals of continuous change of the signal, which cannot be adequately represented by a single point on a time scale. Moreover, one window most often caught change-points from a number of channels.
On the basis of this procedure, the estimation of synchronization can be made in different ways, such as an estimation of synchrony indices for pairs of channels or a search for most frequent multichannel combinations of coinciding change-points. Details of the algorithm may vary in a wide range: for example, in a search for multichannel combinations it is convenient to use fixed windows placed successively one after another along the EEG recording instead of the windows related to change-points.
The number of pairs or multichannel combinations of coinciding change-points can be used in itself as an index of functional coupling of the corresponding brain areas. This number, however, vary with the number of change-points in each channel. Moreover, it may be "contaminated" by randomly coinciding change-points and therefore, in many cases, not give a good idea of the level of non-random coincidence. To get the "purified" estimate, we may subtract an estimate of the number of randomly coinciding change-points pairs or more complex combinations from the actual number of pairs or combinations. The estimate of the random number can be calculated on the basis of the number and distribution of the change-points in each channel. The "purified" estimate can be then normalized in some way dependent on the specific research aims, for example, by division by the minimal or maximal (across the channels) number of change-points, or by the estimate of standard deviation for the randomly coinciding change-points.
Below we discuss the specific methods of the analysis of change-point synchronization and results of their application to the processing of real EEG for the most simple scheme of the analysis, by pairs of channels, and also a number of more complex schemes.