7.4 Experimental results

This section presents the results of the application of the methodology described in the previous section to real EEG signal. The EEG was obtained from human subjects following standard procedures. The subjects were volunteers; all of them gave an informed consent concerning their participation in the experiments. The EEG signal in each EEG channel was registered as a difference of the potential at one of the electrodes applied to scalp and the potential at two electrically connected "reference" electrodes applied to both earlobes (at these sites potential variations are relatively low). Two montages, 8-channel and 16-channel, were used, both in accordance to the standard scheme "10-20". Electrode positions will be shown at the figures illustrating the text below.

To estimate the effects of various brain states, the EEG was recorded when subjects performed different mental tasks and in the rest state, with eyes open or closed. The difference between eyes open and closed states was of special interest, because it greatly modify the alpha band of EEG signal, which was the main subject of the analysis for its sensitivity to mental loading, relatively high power in awake state (in most normal humans) and well time-structured dynamics.

The analog signal was digitized, usually with A/D ratio of 128/s, and processed off-line. The recordings were visually inspected, and only those which contained no large artefacts were used for the analysis. Each EEG channel was processed separately except the final stages of the analysis of change-point coincidence. In most cases, the EEG was bandpass filtered, usually in the alpha band (8--12 or 7.5--12.5 Hz), prior to the change-point analysis.

7.4.1 Change-point detection algorithm performance with real EEG data

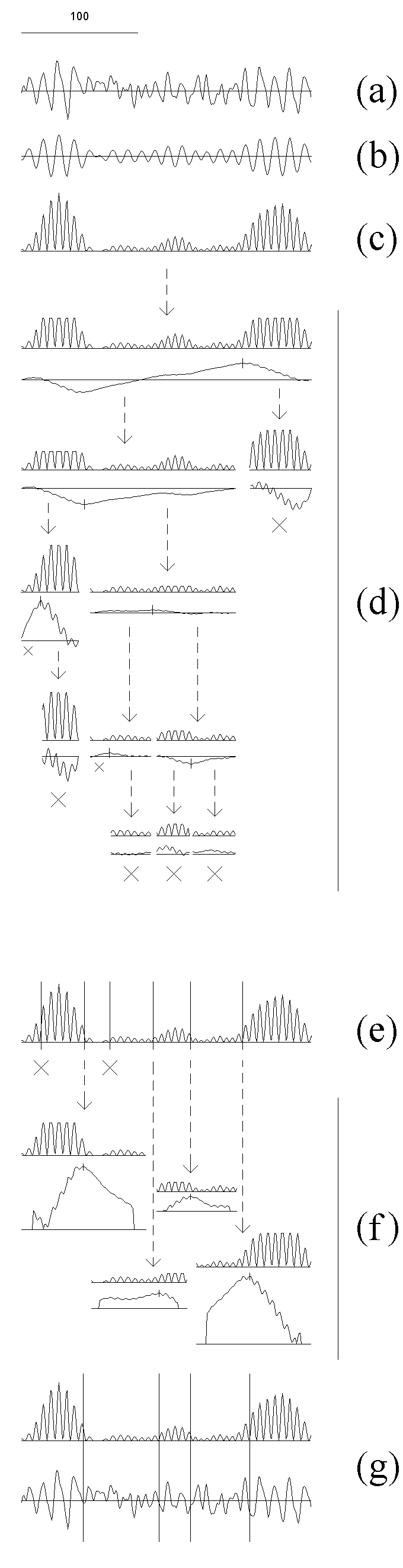
Fig. 7.1. Detection algorithm adapted for the EEG analysis

The EEG (a) was filtered in the alpha band (bandpass 7.5--12.5 Hz) (b) and then the amplitude squared (c); the result is the sequence from which the subintervals are cut out at further steps.

At the next stage (d) the initial interval is sequentially cut into subintervals for which the homogeneity hypothesis is tested and the change-point instants are preliminary estimated. In doing so, the outliers are rejected, and for the resulting sequence (upper curve in each pair) the statistic Y_N(n,1) (lower curve in each pair) and the threshold (not shown) are computed. The threshold at this stage is computed with higher levels of the "false alarm" probability: 0.4, 0.3 and 0.2 for subintervals with length L, L ≥ 100, 50 ≤ L < 100 and 25 ≤ L < 50 samples, correspondingly. If the absolute maximum of the statistic exceeded the threshold, its time instant becomes the preliminary estimate of a change-point (vertical stroke on the curve), and the subinterval is cut into two parts with an break off from it; otherwise the subinterval is considered as stationary and is not analyzed further (large crosses). Too short (less than 25 samples) subintervals also are not analyzed (small crosses). The arrows show how the subintervals are cutting out.

The obtained preliminary change-point estimates are re-examined (e) using the statistic of the same type, but with lower "false alarm" probability, 0.2, 0.1 and 0.05 for subintervals L ≥ 100, 50 ≤ L < 100 and 25 ≤ L < 50 samples, correspondingly. This results in rejecting of some change-points (crosses).

At the final stage (f) the change-point instants are estimated precisely. The subintervals for each of the survived change-points are defined with a small break from the neighbouring change-points, and the outliers are rejected in each subinterval separately (the upper curve in each pair). For each subinterval, a statistic Y_N(n,0) (the lower curve in each pair) is computed, and the time instant of its absolute maximum becomes the final estimate of the change-point instant.

For illustrative purposes, the final change-points instants are shown against the filtered and squared EEG, as well as the original EEG signal, by vertical lines (g).

For more details of the algorithm see Chapters 3 and Appendix.

The sampling (digitizing) rate was 128/s (here and in the further figures, if not specified). Horizontal scale: 100 samples. Vertical scales are in the ratio of 1 (original and filtered EEG) : 250 (diagnostic sequences) : 25 (statistics).

Search for the change-point in power of one of the EEG spectral bands is illustrated in Fig. 7.1. An EEG recording (a) is digitally filtered (b) and transformed into the basic diagnostic sequence (c). The further stages are performed with subintervals of the basic sequence (for details see Chapters 3 and Appendix). In each subinterval the extreme values are "truncated", and then the statistic appropriate for the current stage is computed (Fig. 7.1, d and f). The recording is usually longer than shown at Fig. 7.1, and it can be divided previously into epochs (in our practice, from 200 to 2000 samples each) to be processed separately accordingly to the same schedule.

At the next preliminary stage (Fig. 7.1, d), the homogeneity hypothesis is checked, and preliminary change-point estimates are computed for the subintervals successively extracted from the basic diagnostic sequence. The following is done for each subinterval separately: the outliers are "truncated" on the basis of the distribution for the subinterval, then the statistic Y_N(n,1)and the threshold are computed (everywhere in this Chapter we use the statistics from the basic family (1.4.1)). For the calculation of the threshold at this stage, the "false alarm" probability is set at high level. If the maximum of absolute value of the statistic exceeds the threshold, its instant becomes a preliminary estimate of a change-point, and the subinterval is divided into two parts with receding from it; otherwise the subinterval is considered to be stationary and is not analysed further. Subintervals which are too short also are not analysed.

At the rejection stage (Fig. 7.1, e), for each preliminary change-point estimate a new subinterval is derived from the basic sequence receding from the change-point to each side by 0.9 distance to the neighbouring change-point. In this subinterval, the "truncation" is made, the statistic Y_N(n,1)is computed, and the change-point is checked using lower "false alarm" probability for the calculation of the threshold. Some of the change-points are rejected. At the final estimation stage (Fig. 7.1, f) the subintervals are formed in the same way (they may not differ from the subintervals formed at the previous stage at all, or some of them may become larger due to the rejection of some change-points). A different statistic, Y_N(n,0), is now calculated for each new subinterval, and the maximum of its absolute value becomes the final estimate of a change-point (see Fig. 7.1, f, g).

The EEG fragment shown in Fig. 7.1 exemplifies two features typical for the EEG and its components: 1) the changes often are more or less gradual, i.e., the EEG not completely corresponds to the piecewise stationarity model and, thus, change-points indicated by a detection algorithm are not always the estimates of actual change-points but also may mark non-instantaneous transition processes; 2) even relatively short intervals may include more than one change-points. Although the both features makes the problem of detection more complicated, the procedure is able to divide the EEG successfully into relatively homogenous segments, as is the case for the fragment in Fig. 7.1.